Big-Oh, Big Omega (Ω) and Theta (Θ) notation is commonly seen in analysis of algorithm running times. But many programmers don’t really have a good grasp of what the notation actually means.

In this article you’ll find the formal definitions of each and some graphical examples that should aid understanding.

Big-Oh

The function that needs to be analysed is T(x). It is a non-negative function defined over non-negative x values. We say T(x) is Big-Oh of f(x) if there is a positive constant a where the following inequality holds:

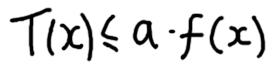
The inequality must hold for all x greater than a constant b.

Example

Using an example on a graph should make it more clear.

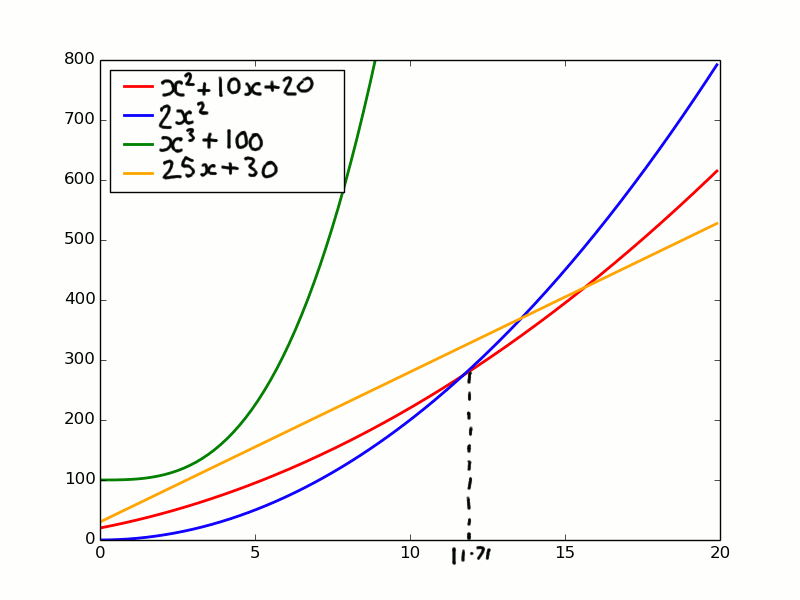
First look at the red line. This is our T(x) that we are analysing. T(x) = x2 + 10x + 20. We want to make Big-Oh statements about this function.

The blue line is 2x2. Notice how the blue line starts lower than the red line. The blue line grows at a faster pace than the red line. It crosses the red line when x is 11.71. After they cross the blue line is always higher than the red line. This means we can say T(x) = Big-Oh(x²) because we have found the two constants needed for the inequality to hold. In this case a = 2 and b = 11.71.

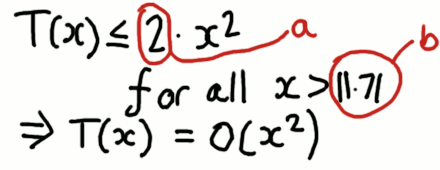
Now look at the green line x3 + 100. We know it is always going to be greater than T(x). So we can say for sure T(x) = Big-Oh(x³ + 100). The constants needed for the inequality in this case are a = 1 and b = 0.

Finally look at the orange line 25x + 30. This line is initially greater than the red line. But as x increases it eventually falls under the red line. You can’t find any constant value of a to satisfy the inequality. Go on try. No matter how large you chose your a there will always be a large enough x where T(n) > 25ax + 100a. So T(x) is not Big-Oh(25x + 30)

Big Omega (Ω)

We say T(x) is Big Omega of f(x) if there is a positive constant a where the following inequality holds:

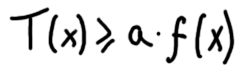
Again the inequality must hold for all x greater than a constant b.

Example

Let’s see how it looks graphically:

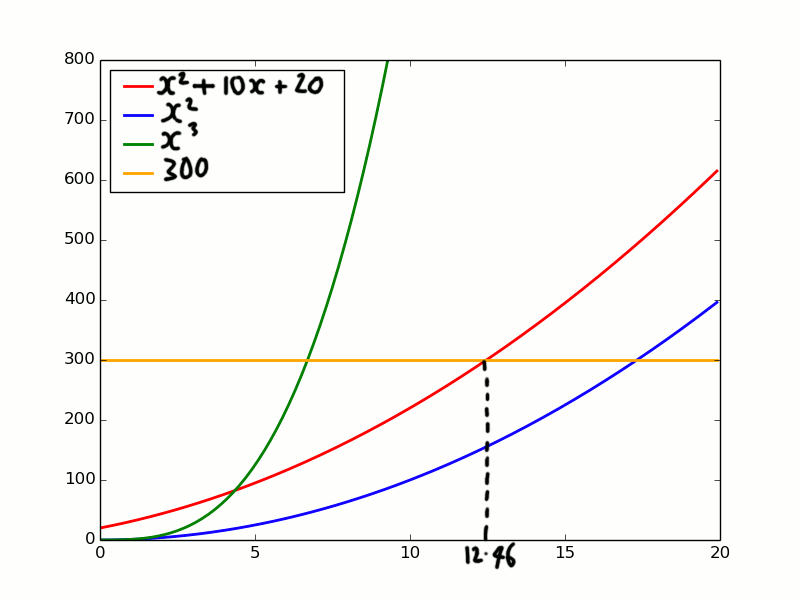
Again the T(x) function we are interested in is the red one. T(x) = x2 + 10x + 20.

First look at the orange line. This is just the constant function f(x) = 300. It starts above the red line. But as x increases the red line grows at a faster rate. When x = 12.46 the red lines crosses the orange line. The orange line is then always under the red line. The above inequality required for Big Omega is therefore satisfied with the two constants a = 1 and b = 12.46. So we can say T(x) = Ω(300).

Look at the blue line. It’s always below the red line. The red line is increasing at a faster pace than the blue line. So we know the blue function will always be less than the red function no matter how large x gets. So we can say T(x) = Ω(x²). In this case the constants that satisfy the inequality are a = 1 and b = 0.

Finally look at the green line x3. This line starts below the red line but it grows at a much faster rate than the red line. This means once the green line goes above the red line we know it will never go below it again. For this reason we can say T(x) is not Ω(x³). You can’t find two constant values for a and b to satisfy the inequality above. No matter how small you choose a the green line will always eventually rise above the red line for some really large x.

Theta (Θ)

We say a function T(x) is Theta(f(x)) if it is both Big-Oh(f(x)) and Big-Omega(f(x)).

Example

Theta is hard to understand at first. But it’s easier to understand if you look at all three elements on the same graph at once. The graph below has the original T(x) function, proof that T(x) = O(f(x)) and proof T(x) = Ω(f(x)):

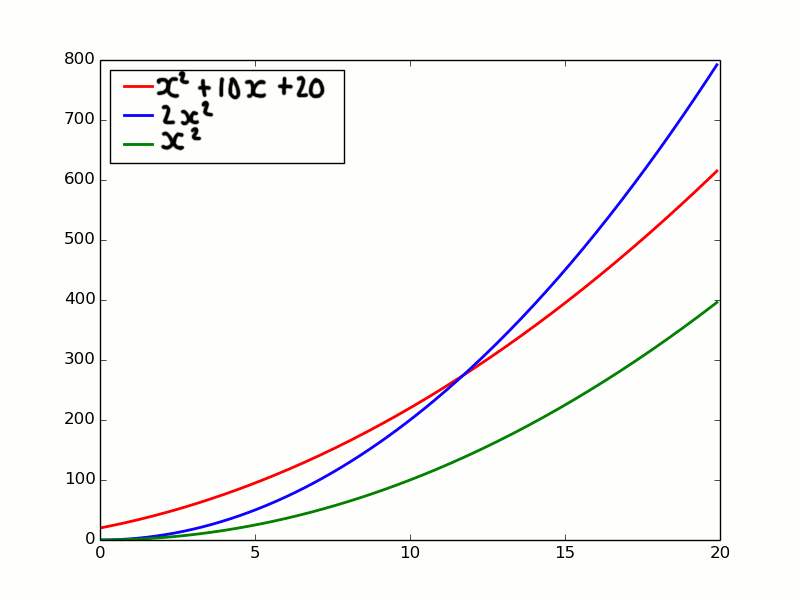
Again the red line is the T(x) function of interest. The blue line demonstrates that T(x) = Big-Oh(x²). The green lime demonstrates that T(x) = Ω(x²). If you don’t think either of these are true go over the definitions for Big-Oh and Big-Omega again. Because T(x) is both Big-Oh(x²) and Ω(x²) we know T(x) = Θ(x²).

A quick rule for finding Theta

The super easy rule for finding a function T(x)’s Theta is:

Take the function T(x). Ignore all leading constant factors. Ignore all terms apart from the highest order term. This is the theta of T(x)

Can you see how this works with the T(x) = x2 + 10x + 20 function that is Θ(x²)?

Little-Oh

Little-oh notation is less commonly used. It is more strict than big-oh notation. We say T(x) is little-oh of f(x) if for all a > 0 the inequality holds:

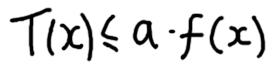
The inequality must hold for all x greater than a constant b.